Why a Fear of Fractions Is Fracturing Students' Future Success in Math
In 1978, more than 20,000 US eighth graders ages 13 and 14 were asked to examine this fractional task:

Then, students were asked to respond to the prompt of whether 1,2,19, or 21 was the closest whole number to the resulting sum.
Only 24% answered correctly (Carpenter, Corbitt, Kepner, Lindquist, & Reys, 1980). What are your thoughts on the correct response? Since both fractions in this addition computation are close to 1, we can surmise that the answer is close to 2. After 40 years of research, policy, and massive investment into improving mathematics teaching throughout the US, one would hope to see a significant increase in our students’ ability to demonstrate an understanding of this question. However, the data is clear — and it’s not pretty: the ability of US students to answer this question correctly has increased to only 27% as of 2018. If you just made a noise with your mouth, you are not alone.
The struggle with fractions is nothing new, and if you suffer from this malaise, you’re not alone, and there is nothing wrong with you (Behr, Lesh, Post, & Silver, 1983; Siemon et al., 2015). The consequences of low flexibility in working with fractional quantities are huge barriers to learning and developing higher-order mathematical thinking. The mental barriers of fearing elementary mathematics are crippling to adults and children. Fractional fluency has much to do with the cognitive processes of proportional and spatial reasoning (Moss & Case, 1999). Would you believe that your ability to learn and develop fluency with fractions directly predicts your ability to learn Algebra flexibly? (Siegler, et. al, 2012). Algebra, currently the gateway to all further STEM and scientific studies, is the vital application of numbers and operations where the number is “unknown.” Algebra is also the single fracture point for diversifying all STEM industries and occupations regarding race, gender, and socio-economic status (Kaput, 2000).
So, if we pause for a moment, it becomes clear that early struggles with fractions can close off your access as a human to many high-paying, high-impact industries for your career. Fractions are essential, but for many of us, trying to understand this crucial concept leaves us stuck in a mental freeze. It doesn’t have to be this way; let’s unpack that.
WE INVENTED FRACTIONS, TELL THEM WHO IS BOSS…
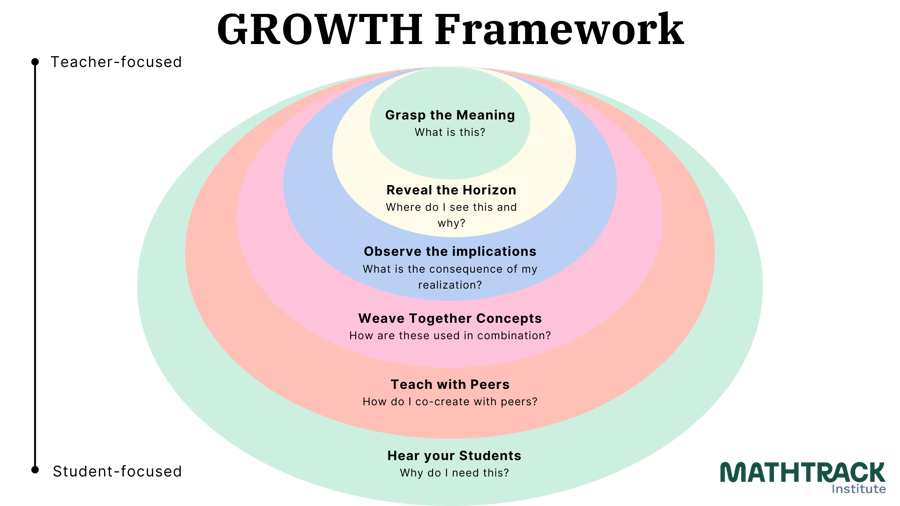
A key part of MathTrack Institute's GROWTH framework for developing knowledgeable and effective mathematics teachers is understanding the historical context of mathematical concepts. This is part of “G” in GROWTH, or Grasp the Meaning. Realizations are everything that gives a mathematical concept meaning. Mathematical concepts, like humans, have a history, and understanding that history makes a deeper understanding possible.
Fractions were included in the first written accounts of symbolic systems (Struik, 1987). More complex mathematics, beyond primitive record keeping and counting, appeared in written records between 5000 and 3000 BC (Eves, 1997). The Egyptian system for whole numbers was not a place value system, while the Sumerian and Babylonian systems were (Flegg, 1989). Egyptian reliance on unit fractions (1 in the numerator) complicated representations and computations with fractional measures. For example, the number ¾ would have been written as ½ + ¼, and then computations on this number would have been accomplished by dealing with the two unit fractions. It may seem strange today, but the use of the Egyptian system for the representation and computation of fractional quantities lasted into the 1400-1500s AD (Flegg, 1989). For context, humanity struggled with fractions for thousands of years, and now we teach them to 8-year-olds. Progress! However, the unintended consequence of mass access to concepts that used to be only for the elite is that we need to understand them better so that we can teach them to everyone. Your anxiety, if you have it, in dealing with fractions is because we haven’t evolved into this potential yet.
THE FIRST ABSTRACTION
The next stages of the GROWTH framework are about understanding the concept in the context of the curriculum and its implications for understanding it in certain ways. This is the (ROW), “Reveal the Horizon,” “Observe the Implications,” and “Weave together Concepts” part of GROWTH.
Fractions are arguably one of the most complex and nested abstractions introduced in elementary mathematics. There is a reason that it is difficult, and a well-trained educator in the classroom is vital. Fractions represent a real leap from the careful and often overly burdensome introduction to whole numbers and operations on whole numbers in elementary school. Susan Lamon (1999) identified four different representations of fractions: (a) fractions as symbols, (b) part-whole fractions, (c) fractions as rational numbers, and (d) fractions as numbers. Four different representations! These are all nuanced and all part of how children are introduced to fractions. Here is a brief explanation of each:
Fractions as symbols. A fraction can be understood as writing a pair of numbers. I know that might sound strange, but can you think of a situation where a kid was asked to write two ones and wrote eleven? At an early stage of development in literacy, it’s hard to understand a letter as a symbol, something that makes a sound, and something that has meaning. Same idea here. Lamon (1999) stated that the word “fraction” can be used as a symbol for writing a number, a notational system, a symbol, and two numbers with a bar between them” (p. 27).
Part-whole fractions. This is the first interpretation of fractions that children are exposed to throughout the elementary curriculum (Lamon, 1999). Without a confident educator, this can be the only interpretation students carry into adulthood. A fraction, as a ratio of part to whole, refers to one or more parts of a unit that have been divided into some number of equal-sized parts. So, 6/8 can be understood as the ratio of six parts out of the total of 8 equal parts of some decided upon whole (pizza, cups, aardvarks, the ocean). If you notice, the assumption here is that fractions can be linked to the intuitive ideas derived from the “division” idea of fair-sharing. This works quite well for “proper fractions” like 2/12, but what does it mean to have 14/12? The phrase 14 parts out of 12 is confusing to anyone, or at least should be.
Fractions as rational numbers. In mathematics, a rational number is a number that can be expressed as the quotient (division) of two integers (positive and negative whole numbers), a numerator p, and a non-zero denominator q. Fractions as rational numbers allow individuals to “talk about wholes as well as pieces of a whole” (Lamon, 1999, p. 28). This conception of fractions is useful because 24/4 is a fraction, but it also means six whole groups of four parts of 24 (4+4+4+4+4+4). However, it brings other complexities because it requires educators to have a deeper understanding of the mathematics for teaching underpinning this concept. This deeper understanding would allow a teacher to understand that the word fractions and rational numbers are not coterminous or interchangeable. For example, all fractions are not rational numbers and do not correspond to different rational numbers. An easy example of this would be π /1 . This is a fraction but not a rational number because π, by its definition, is not a rational number. Or if you don’t like π (who doesn't like pie?), how about 7/0. That is also not a rational number, but it is a fraction.
Fractions as numbers. When considering a fraction as a number, the user refers to the underlying rational number, the number that the fraction symbol represents (Lamon, 1999). The complexity here is that fraction as a number is a relative term. For example, 6/8 can be understood as a number, like all other infinite variations of 6/8, such as ¾, 18/24, or 8100/10800. They each equal the same value or referenced quantity. The elementary exposure to fractions as parts of whole numbers, especially the geometric and food representations students are inundated with in elementary mathematics, limits their conceptual understanding (Kerslake, 1986; Hannula, 2003). There is a deeper understanding that is extremely useful, though it takes the utility of fractions beyond measuring cups. In later mathematics, thinking about the number 12 flexibly, especially in the fraction form, becomes an irreplaceable utility for solving complex problems and models for complex problems.
YOU NEED TO TRY IT
One of the GROWTH framework's most important facets is that you must try things out and then share the outcomes with others. This is the (TH) “Teach with Peers” part of GROWTH and the “Hear your Students” part. Teaching is not talking to children about mathematics; it’s about sharing a learning experience with them and listening to their thoughts, questions, feelings, and reactions. You can do this as a parent or a professional mathematics educator. Let’s try this together on some fraction tasks. Remember, this isn’t about anything other than you trying and reflecting on how it feels. For some of us, this will be uncomfortable. You cannot teach well if you do not have empathy for how it feels to learn something difficult. The following exercises are sampled from research about fractions over the last 50 years.
To start, let’s examine what you would call the fraction represented in the diagram below. Again, if your palms are getting sweaty, don’t worry — there is no wrong answer. The point is that we learn together more about what we will be helping others learn.

The most common incorrect responses to this task come from the different representations of fractions that we discussed above. If you confused the part and the whole, you would state that this is 7/10 rather than 7/5. In a diagram like this, the whole is represented by the area of the rectangle. This means two wholes are given, one full and the other partly full. Since the area is conveniently cut into 5ths for you, you can count the total number of 5ths shaded in and state that out of the whole, which has 5 total parts for one whole.
Here is a second exercise—the same goal of achieving flexibility using and recognizing fractional quantities. The given diagram is designed to represent the addition of two proper fractions. Write down the fractions represented. Then, try to add these quantities together into one fractional quantity.

If you have difficulties with part-whole representations of fractions, looking at this diagram, similar to the first exercise, you might try to work through that this is 5/7. But each of these diagrams was given as separate quantities, so the first rectangle is ⅔, and the second rectangle represents ¾. Now that you clearly understand the fractional quantities given, you can ask yourself what it would mean to combine them—combining means adding them together using the addition operation. So, a better question would be, what does it mean to add ⅔ and ¾ together? What “number” do you use to label that new quantity? To add these, you must find parts of a whole that will help you combine both numbers. If the division sizes are the same in both representations of fractions, then you can count them and talk about the final quantity. You likely remember this as finding a common denominator, but let’s avoid that language for now.

or

The previous representations and the new names that we are about to come up with are the same “quantities,” but we will call them different numbers (8/12 and 9/12), respectively. With fluency in fractions, you can find equal quantities represented by an infinite number of fractions. In this case, what a common multiple of 3 and 4 would produce a number that both 3 and 4 have in common. The smallest of these is 12, so we can use our new fractions, which represent the same quantities as our original fractions, will be in terms of 12ths, as shown above. So our whole is 12ths, and counting up all our parts is 17. So, the final solution is that ⅔ + ¾ = 17/12.
Remember, this is about learning more and testing these ideas with others. Our work together is to build confidence. If you fear fractions, you cannot use them to enhance your way of approaching the world or effectively teach children how not to fear these concepts. Fluency without fear isn’t just a fun phrase; it’s our goal in working with you and talking about these concepts.
CALL TO COLLABORATE
MathTrack’s GROWTH framework is designed to support parents as well as new, novice, and master teachers to continue to deepen and enrich their understanding of their craft (teaching kids). We aim to build confidence, and we all want more confident and effective teachers in our classrooms working with our children. If you, as a school leader or teacher, want to raise the confidence of mathematics teaching in your classrooms, please contact our team. We would be happy to support you with questions that you may have and feedback about our framework.
ABOUT MATHTRACK INSTITUTE
MathTrack Institute focuses exclusively on math-specific training, offering a transition to teaching (T2T) licensure program, an apprenticeship-based Bachelor’s degree, and professional development thoughtfully designed for aspiring, novice, and experienced math teachers. Driven by their innovative GROWTH framework, they’re on a mission to help schools fill talent pipelines from within their communities for qualified math teachers now and later. MTI is headquartered in Indianapolis, with programs available nationally.
Subscribe to Our Newsletter