The Age of Mathematical Storytellers
MathTrack's GROWTH Framework™ helps educators become what our classrooms and communities need most—storytellers of mathematics. This isn’t a set of strategies. It’s a way of seeing, knowing, and teaching that brings mathematics to life.
Find our book on Amazon (link)

To teach mathematics is not simply to deliver content-- it is to participate in a deeper cultural story.
In a time of automation and acceleration, what remains uniquely human is our ability to connect, interpret, and shape meaning. That’s what storytelling does. And that’s what the GROWTH Framework invites teachers to do—with mathematics as the narrative.
Each movement in GROWTH is a rhythm of sensemaking. Not steps. Not scripts. But tools for becoming. Teachers use the GROWTH Framework to deepen their practice, refine their storytelling, and awaken their students’ curiosity.
The GROWTH Framework™: Storytelling in Mathematics
The GROWTH Framework™ empowers educators to transform mathematics into a compelling narrative, enriching both teaching and learning experiences. By focusing on self-discovery, collaborative insights, and meaningful connections with students, the framework helps educators embrace their role as storytellers, weaving mathematics into the fabric of their communities
The MathTrack GROWTH Framework™
The GROWTH Framework™ Movements
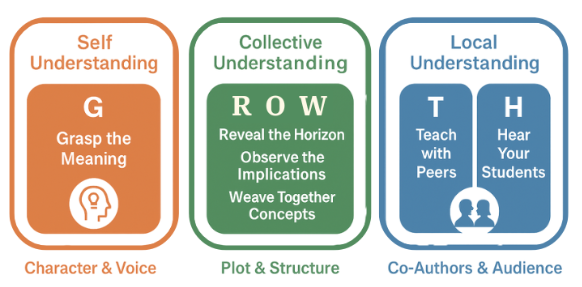
Principle 1: Grasp the Meaning
Uncovering the “Characters” of Mathematics
Teaching begins not with what you teach, but how you see. “Grasp the Meaning” is about developing an intimate understanding of a mathematical concept—its definitions, its visual forms, its behavior, and its relevance.
"Just like a storyteller knows their characters, a math teacher must come to know their concepts as deeply lived ideas."
What it looks like: Teachers explore multiple representations, develop narrative arcs for concepts such as fractions or exponents, and connect ideas to human experiences, emotions, and cultural meanings.
Principle 2: Reveal the Horizon
Seeing the Arc of the Story
Every concept lives within a broader arc. “Reveal the Horizon” invites educators to develop mathematical peripheral vision—to understand where ideas originate, what they connect to, and how they evolve over time and across grade levels.
"Great storytellers know what came before and what’s coming next. So do great teachers."
What it looks like: Teachers design learning experiences that anticipate future struggles, plant seeds of insight, and highlight the long arc of reasoning across the curriculum.
Principle 3: Observe the Implications
Exploring the "Rules of the World"
Mathematics, like any good story, is filled with tension and contradiction. “Observe the Implications” helps educators and students explore what happens when mathematical concepts meet different contexts—what breaks, what holds, and what that teaches us.
"Dignity in teaching comes from honoring the contradictions, not hiding them."
What it looks like: Teachers model curiosity, welcome student struggle, and use conceptual shifts as openings for insight. Students begin to see that understanding grows at the edges of what they thought they knew.
Principle 4: Weave Together Concepts
Building Coherent Narratives
No idea in mathematics lives alone. “Weave Together Concepts” is the movement of synthesis—helping students and teachers connect concepts across domains, disciplines, and lived experiences.
"Every concept is a character in a shared world. The teacher’s role is to help build the map."
What it looks like: Teachers use analogies, timelines, and thematic storytelling to connect geometry to algebra, or data to decisions. Students begin to see mathematics not as fragments, but as an unfolding story.
Principle 5: Teach with Peers
Collaboration as a Catalyst for GROWTH
Teaching is a communal act. “Teach with Peers” reminds us that growth accelerates when we work together. When teachers collaborate, they not only refine their methods—they enrich their identities as educators and storytellers.
“You are already a storyteller. Let’s make it intentional. Let’s make it shared.”
What it looks like: Teachers engage in co-planning, reflective dialogue, and peer feedback. Through shared metaphors and collaborative sensemaking, they discover new stories, new structures, and new confidence.
Principle 6: Hear Your Students
Students as Co-Authors of the Story
To teach mathematics well is to listen with care. “Hear Your Students” reframes assessment and feedback as opportunities to understand the student’s story—how they think, where they hesitate, and what they believe about themselves.
"The classroom is not your stage-- it's a shared space of narrative construction."
What it looks like: Teachers tune into the emotional and intellectual rhythms of student thinking. They respond not just with correction, but with compassion, scaffolding, and invitations to deepen the story together.
The Research Behind GROWTH
A Narrative Informed by Practice, Cognitive Science, and Complexity Thinking
The GROWTH Framework didn’t begin as a checklist or a curriculum.
It was born from a research agenda focused on one central question: How do teachers make meaning in mathematics—and how do they help students do the same?
Over two decades, the architects of GROWTH investigated how knowledge is constructed, transferred, and embodied in the classroom. The result is a framework grounded in three overlapping traditions:
Cognitive Science and Learning Sciences
Researchers such as Ball, Thames, and Bass, as well as Davis and Simmt, have helped shape what we now call "mathematical knowledge for teaching"—the nuanced, practice-based knowledge that teachers use in real-time. Their work emphasized:
- The tacit knowledge teachers draw upon in the moment
- The relational complexity of interpreting student thinking
- The pedagogical moves that signal deep understanding
These insights laid the foundation for "Grasp the Meaning" and "Hear Your Students."
Sensemaking and Complexity Theory
From the organizational lens, theorists like Dave Snowden and Max Boisot explored how knowledge moves, evolves, and resists simplification.
- Snowden's Cynefin Framework is a tool used for decision-making, categorization of situations, and understanding the nature of complex systems.
- Boisot's I-Space Model explains how tacit, abstract, and codified knowledge must be balanced to support innovation and learning.
This body of research shaped the "Teach with Peers" and "Weave Together Concepts" movements—where knowledge is co-constructed, not simply delivered.
Educational History and Philosophy
Drawing on thinkers such as Dewey, Harari, and Labaree, the GROWTH Framework positions teaching as a cultural act, not just a technical one.
- Harari's theory of intersubjective reality explains how shared myths (such as school, mathematics, justice, and money) are sustained through storytelling.
- Labaree reminds us that teacher education has long struggled to strike a balance between rigor and relevance. The GROWTH Framework restores this balance by making meaning-making central.
These ideas are the philosophical heart of the GROWTH Framework and the Age of Storytellers.
Why It Matters Now
In the Age of AI, what makes human teachers essential is not their ability to recite content—but their ability to build narrative coherence, respond to the messiness of real thinking, and guide students through uncertainty with insight and care.
That’s what the GROWTH Framework does.
It develops teachers as storytellers: sensemakers, editors, and cultural stewards—a role that no algorithm can replace.
Bring the GROWTH Framework™ to your School and Classroom
Ready to teach mathematics with purpose, power and story?
We offer degree programs, apprenticeships, professional development, fellowships, and site-based coaching using the GROWTH Framework™ and The Age of Storytellers as foundational tools.

